Cho một bảng hình vuông kích thước 2 × N - 1. Các số bắt đầu từ 1 được viết vào các ô của bảng theo thứ tự từ ngoài vào trong, chia thành N vòng:

• Vòng 1: chỉ gồm 1 ô vuông ở trung tâm bảng.
• Vòng 2: gồm 8 ô vuông bao quanh vòng 1.
• Vòng 3: gồm 16 ô vuông bao quanh vòng 2.
• …
• Vòng N: gồm các ô vuông ở rìa ngoài cùng của bảng.

Hình dưới đây mô tả bảng với N = 4:

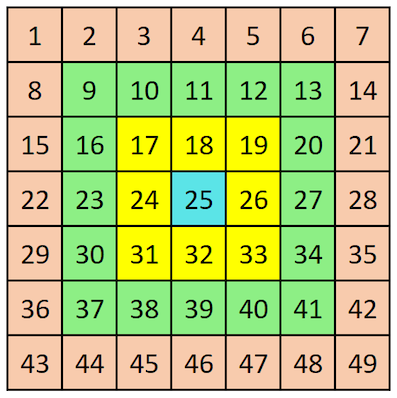
Bài Toán

Cho số nguyên dương K. Hãy tính tổng các số có trong vòng thứ K của bảng.

Input Specification

• Dòng 1 chứa số nguyên N (1 ≤ N ≤ 10^9).
• Dòng 2 chứa số nguyên dương K (K ≤ N).

Output Specification

• Vì kết quả có thể rất lớn nên chỉ cần in ra phần dư của tổng tìm được khi chia cho 10007.

Sample Input

4
2

Sample Output

200

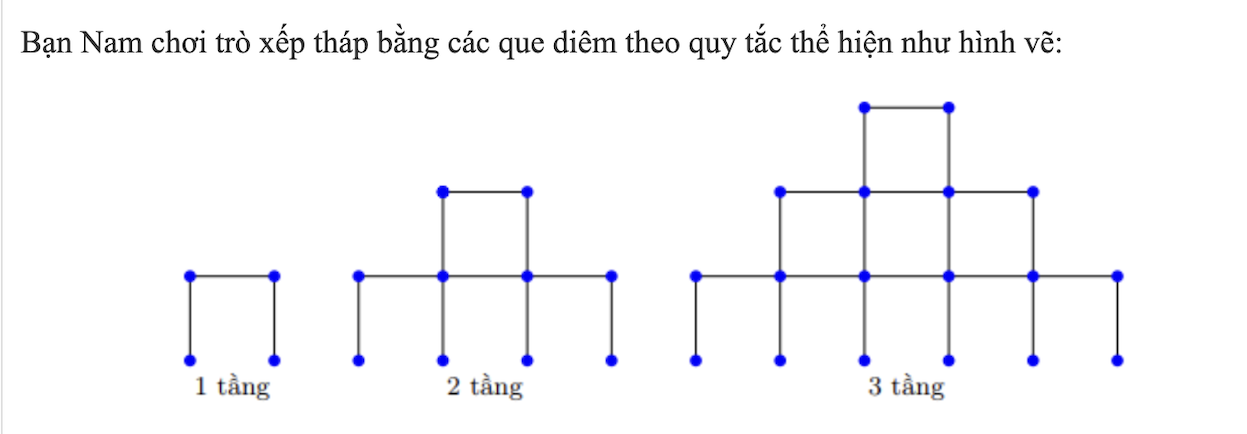
Bạn Nam có N que diêm thì có thể xếp được tháp cao nhất là bao nhiêu tầng ?

Input:

Nhập vào một số nguyên dương N (1 <= N <= 10^12)

Output:

Tầng tháp cao nhất

Ví dụ 1:

Input:

10

Output:

2

Đếm số que diêm

Cho t test case. Mỗi test case gồm hai số nguyên l, r.

Với mỗi số i trong khoảng [l, r], ta xác định số que diêm cần để hiển thị i trên màn hình bảy đoạn:

• Số que diêm của mỗi chữ số 0–9:

  

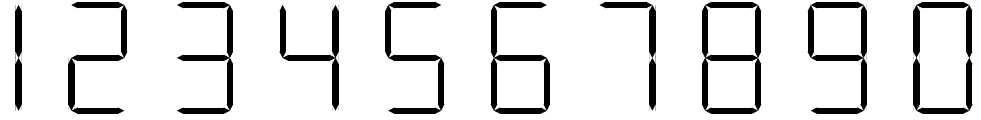
Hãy tìm số que diêm ít nhất và nhiều nhất cần dùng trong khoảng [l, r].

Input

• Dòng đầu chứa số nguyên t (số test case).
• Mỗi test tiếp theo gồm hai số nguyên l và r (1 ≤ l ≤ r ≤ 10^5).

Output

Với mỗi test case, in ra hai số: số que diêm nhỏ nhất và số que diêm lớn nhất trong khoảng.

Ví dụ

Input

1
1 10

Output

2 8

Một số nguyên dương được gọi là số đối xứng (palindrome) nếu khi viết các chữ số của nó (trong hệ thập phân) theo thứ tự ngược lại ta vẫn được chính số đó.

Cho 2 số nguyên dương l, r, đếm xem có bao nhiêu số đối xứng trong đoạn [l, r].

Input

• Gồm một dòng ghi hai số nguyên dương l và r cách nhau bởi dấu cách.

Giới hạn

• 1 ≤ l ≤ r ≤ 10¹⁵, và r - l ≤ 10⁵.

Output

• In ra số lượng số đối xứng trong đoạn [l, r].

Ví dụ 1

Input:
1 10


Output:
9

Ví dụ 2

Input:
11 30


Output:
2

Bình đang chơi một trò chơi năng lượng. Ban đầu Bình có E điểm năng lượng. Mỗi ngày bắt đầu, năng lượng của Bình giảm đi 3 điểm. Sau mỗi T ngày, Bình nhận thêm R điểm năng lượng (sau khi đã trừ 3 điểm của ngày đó). Hỏi nếu không nạp thêm năng lượng thì đến ngày bao nhiêu Bình không thể chơi tiếp (khi bắt đầu ngày mà năng lượng < 3 thì không chơi được) ?

Nếu Bình không bao giờ hết năng lượng, in ra -1.

Ràng buộc

• (1 <= E <= 10^9)
• (0 <= R <= 10^5)
• (1 <= T <= 10^6)

Dữ liệu vào

• Dòng 1: số nguyên E — năng lượng ban đầu.
• Dòng 2: số nguyên R — năng lượng nhận được sau mỗi (T) ngày.
• Dòng 3: số nguyên T — chu kỳ nhận năng lượng (ngày).

Dữ liệu ra

• Một số nguyên: số ngày Bình không thể chơi tiếp, hoặc -1 nếu không bao giờ cạn.

Ví dụ

Input:
20
4
3

Output:
11

Giải thích:

• Ngày 1: 20-3=17
• Ngày 2: 17-3=14
• Ngày 3: 14-3=11 → nhận +4 → 15
• Ngày 4: 15-3=12
• Ngày 5: 12-3=9
• Ngày 6: 9-3=6 → nhận +4 → 10
• Ngày 7: 10-3=7
• Ngày 8: 7-3=4
• Ngày 9: 4-3=1 → nhận +4 → 5
• Ngày 10: 5-3=2
• Ngày 11: vì 2 < 3 không đủ năng lương chơi tiếp → dừng

Số ngày không chơi được: 11.

Sau khi vượt qua một bài kiểm tra, Vasya nhận được một hộp gồm n viên kẹo. Cậu quyết định mỗi buổi sáng ăn một lượng kẹo cố định cho đến khi hộp hết kẹo. Tuy nhiên, Petya cũng để ý đến hộp kẹo và muốn lấy cho mình một phần.

Quá trình diễn ra như sau:

1. Ban đầu, Vasya chọn một số nguyên k (cố định suốt các ngày).
2. Vào mỗi buổi sáng, Vasya ăn k viên kẹo từ hộp (nếu còn ít hơn k viên thì ăn hết).
3. Vào mỗi buổi tối, Petya ăn 10% số kẹo còn lại trong hộp. Nếu số kẹo không chia hết cho 10, Petya làm tròn xuống. Ví dụ, nếu còn 97 viên, Petya chỉ ăn 9 viên; nếu còn dưới 10 viên, Petya không ăn viên nào.
4. Nếu hộp vẫn còn kẹo, lặp lại từ bước 2 với cùng giá trị k.

Cho trước số kẹo ban đầu n, hãy tìm giá trị nguyên k nhỏ nhất sao cho Vasya sẽ ăn được ít nhất một nửa số kẹo ban đầu (tức là >= ⌈n/2⌉ viên).

Input

Dòng đầu tiên chứa một số nguyên n (1 ≤ n ≤ 10^18) — số viên kẹo ban đầu trong hộp.

Output

In ra một số nguyên duy nhất — giá trị k nhỏ nhất để Vasya có thể ăn được ít nhất một nửa số kẹo ban đầu.

Ví dụ

Input:
68

Output:
3

Giải thích mẫu

Với n = 68 và k = 3, quá trình thay đổi số kẹo trong hộp (Vasya ăn trước) như sau:

68 → 65 → 59 → 56 → 51 → 48 → 44 → 41 →
37 → 34 → 31 → 28 → 26 → 23 → 21 → 18 →
17 → 14 → 13 → 10 → 9 → 6 → 6 → 3 → 3 → 0

Tổng cộng Vasya ăn được 39 viên, Petya ăn 29 viên, nên Vasya đã ăn ít nhất một nửa (34) của 68.