Cho một bậc thang số vô hạn sao cho:

• Hàng thứ k có đúng k ô, đánh số liên tiếp bắt đầu từ 1.
• Số ghi trong các ô là các số nguyên dương liên tiếp, điền theo hàng.
• Với hàng chẵn thì điền từ trái sang phải.
• Với hàng lẻ thì điền từ phải sang trái.

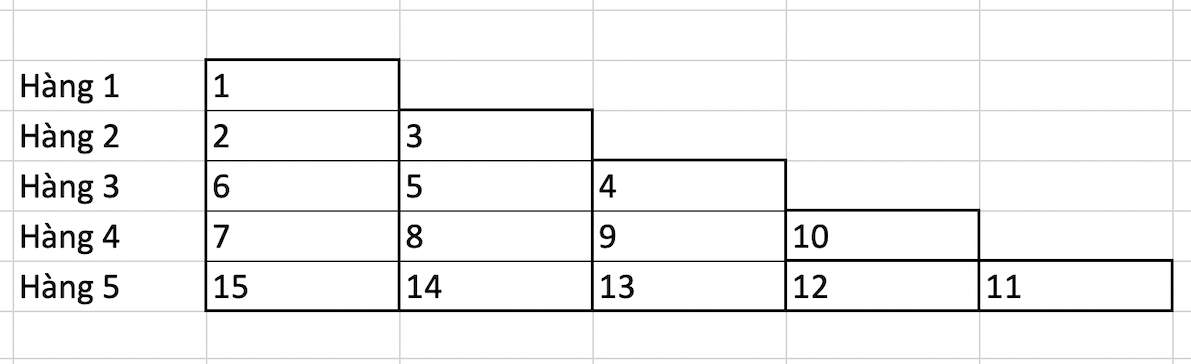
Ví dụ, 5 hàng đầu của bậc thang được điền như sau:

Hàng 1 (lẻ):        [1]
Hàng 2 (chẵn):     [2] [3]
Hàng 3 (lẻ):    [6] [5] [4]
Hàng 4 (chẵn): [7] [ 8] [ 9] [10]
Hàng 5 (lẻ):[15] [14] [13] [12] [11]

Viết chương trình trả lời hai truy vấn:

1. Cho số A (1 ≤ A ≤ 10^12), xác định A nằm ở hàng thứ mấy và ô thứ mấy (từ trái sang phải).
2. Cho hai số R, C (1 ≤ C ≤ R ≤ 10^9), tìm giá trị của ô ở hàng R, cột C (từ trái sang phải).

Input:

• Dòng 1: Số nguyên A.
• Dòng 2: Hai số nguyên R và C.

Output:

• Dòng 1: Hai số cách nhau một khoảng trắng: số hàng của A và số ô của A.
• Dòng 2: Một số nguyên là giá trị tại ô hàng R, cột C.

Input:

9
5 2

Output:

4 3
14

Cho hai số tự nhiên X và N, hãy đếm xem có bao nhiêu số tự nhiên Y thỏa mãn:

• Y <= N

• Tích của hai số X và Y chia hết cho 10.

• Hãy lập chương trình cho phép nhập vào 2 số X và N. (X, N <= 10^9), sau đó đưa ra số lượng số Y thỏa mãn yêu cầu đề bài:

*Ví dụ: *

• X = 3 và N = 20 thì đưa ra kết quả là 2
• Giải thích: Vì 3 x 10 = 30 chia hết cho 10 và 3 x 20 = 60 chia hết cho 10.

Test case mẫu

Đầu vào mẫu 1

3
20

Đầu ra mẫu 1

2

Nguyên viết dãy số theo quy tắc sau:

• Bắt đầu từ số 1, nhân đôi số đó và cộng 4, được số thứ hai là 6.
• Lặp lại quá trình này, bắt đầu với số cuối cùng trong dãy, nhân đôi rồi cộng 4, nhưng Nguyên chỉ viết chữ số hàng chục và đơn vị nếu số đó lớn hơn 100.

Hãy tìm số thứ N và tổng N số đầu tiên mà Nguyên đã viết.

Input

Một số tự nhiên N (1 ≤ N ≤ 10^12).

Output

Dòng 1 gồm 1 số nguyên là số thứ N Nguyên đã viết. Dòng 2 gồm 1 số nguyên là tổng N số đầu tiên Nguyên viết.

Ví dụ 1:

Input:

2

Output:

6
7

Ví dụ 2:

Input:

5

Output:

76
135

Hướng tới kỉ niệm 30 năm hội thi Tin học trẻ toàn quốc năm 2024, Thành Đoàn Hà Nội tổ chức sân chơi cho các em học sinh của Thủ đô. Trò chơi đầu tiên là biến đổi số.

Cho số X ban đầu có n chữ số a₁a₂…aₙ₋₁aₙ. Liên tục thực hiện phép thay thế X bởi X mới theo quy tắc sau:

• Lấy chữ số cuối cùng của số X nhân với 30 rồi cộng vào phần X sau khi đã xóa chữ số cuối cùng.
• Nếu X chỉ còn một chữ số thì giữ nguyên, không cần biến đổi.

Nghĩa là: Xₘới = aₙ × 30 + a₁a₂…aₙ₋₁

Hãy giúp ban tổ chức đưa ra số X cuối cùng sau khi thực hiện K phép biến đổi.

Dữ liệu vào từ bàn phím:

• Dòng 1: chứa số tự nhiên X là số ban đầu (1 ≤ X ≤ 10^15).
• Dòng 2: chứa số tự nhiên K là số lần biến đổi (1 ≤ K ≤ 10^16).

Kết quả ra màn hình:

• Một dòng chứa một số tự nhiên là kết quả.

Ví dụ:

Input 1:

12
2

Output 1:

36

Giải thích:

Lần 1: 2 × 30 + 1 = 61
Lần 2: 1 × 30 + 6 = 36

Input 2:

100
2024

Output 2:

1

Giải thích:

Lần 1: 0 × 30 + 10 = 10
Lần 2: 0 × 30 + 1 = 1
Từ lần 3 chỉ còn một chữ số, giữ nguyên.

Limak chuẩn bị tham gia một cuộc thi vào ngày cuối cùng của năm 2016. Cuộc thi bắt đầu lúc 20:00 và kéo dài bốn giờ, chính xác đến nửa đêm. Sẽ có n bài toán, sắp xếp theo độ khó, tức bài 1 là dễ nhất và bài n là khó nhất. Limak biết cậu ấy sẽ mất 5 * i phút để giải bài toán thứ i.

Bạn của Limak tổ chức một bữa tiệc đêm giao thừa và Limak muốn có mặt ở đó vào lúc nửa đêm hoặc sớm hơn. Cậu ấy cần k phút để đi từ nhà đến bữa tiệc.

Hỏi Limak có thể giải tối đa bao nhiêu bài toán để kịp đến bữa tiệc?

Input:

Dòng duy nhất của đầu vào chứa hai số nguyên n và k (1 ≤ n ≤ 10, 1 ≤ k ≤ 240) — số bài toán trong cuộc thi và số phút Limak cần để đến bữa tiệc từ nhà.

Output:

In ra một số nguyên, biểu thị số bài toán tối đa Limak có thể giải để đến bữa tiệc trước hoặc đúng lúc nửa đêm.

Ví dụ 1:

3 222

Output:

2

Input:

4 190

Output

4

Input

7 1

Output

7

Giải thích

• Trong ví dụ đầu tiên, có 3 bài toán và Limak cần 222 phút để đến bữa tiệc. Ba bài toán lần lượt yêu cầu 5, 10 và 15 phút. Limak có thể dành 5 + 10 = 15 phút để giải hai bài đầu tiên. Sau đó, vào 20:15 cậu có thể rời nhà để đến bữa tiệc vào lúc 23:57 (sau 222 phút). Trong trường hợp này Limak sẽ giải được 2 bài. Cậu không còn đủ thời gian để giải 3 bài nên đáp án là 2.

• Trong ví dụ thứ hai, Limak có thể giải cả 4 bài trong 5 + 10 + 15 + 20 = 50 phút. Vào 20:50 cậu sẽ rời nhà và đến bữa tiệc. Cậu sẽ đến đúng vào lúc nửa đêm.

• Trong ví dụ thứ ba, Limak chỉ cần 1 phút để đến bữa tiệc. Cậu có đủ thời gian để giải cả 7 bài.

Cho số tự nhiên A có N chữ số và số tự nhiên B có M chữ số (2 ≤ N, M ≤ 200). Số nguyên dương C gồm các tính chất sau đây:

• Có N + M chữ số;
• Được tạo bởi từ các chữ số của A và B;
• Thứ tự trước sau các chữ số của B trong C không thay đổi.

Yêu cầu: Tìm số C nhỏ nhất và số C lớn nhất.

Input:

Dòng đầu ghi số A. Dòng tiếp theo ghi số B.

Output:

• Dòng đầu ghi số C nhỏ nhất
• Dòng tiếp theo ghi số C lớn nhất

Ví dụ:

Input:

20
4181

Output:

204181
421810