TICA - Kỳ Thi Tết Trung Thu 2025 - Tối thứ 7
Phát Kẹo Trung Thu
Nộp bàiPoint: 100
Phát kẹo Trung Thu
Nhân dịp Tết Trung Thu, Thầy Thịnh phát kẹo cho các bạn học sinh theo hàng từ trước ra sau.
Quy tắc phát kẹo như sau:
- Bạn đầu hàng nhận 1 viên kẹo.
- Mỗi bạn tiếp theo nhận nhiều hơn bạn đứng ngay trước 3 viên.
Hỏi nếu có N học sinh thì tổng số kẹo Thầy Thịnh cần chuẩn bị là bao nhiêu?
Input
- Một số nguyên dương N — số học sinh trong hàng.
Output
- In ra một số nguyên duy nhất là tổng số kẹo Thầy Thịnh phải chuẩn bị.
Ràng buộc
- 1 ≤ N ≤ 10^9.
Ví dụ
Ví dụ 1
Input
1
Output
1
Ví dụ 2
Input
3
Output
12
Giải thích: Lần lượt các bạn nhận 1, 4, 7 viên → tổng 1 + 4 + 7 = 12.
Hành trình ngắn nhất
Nộp bàiPoint: 100
Câu 1: Hành trình ngắn nhất
Hàng ngày hành trình của An là từ nhà đi đến trường. Khi học xong ở trường An luôn đi đến thư viện tỉnh đọc sách và tự học. Cuối ngày, khi kết thúc việc đọc sách ở thư viện An đi về nhà mình.
Có ba con đường:
- Con đường thứ nhất từ nhà An đến trường có độ dài
a(đơn vị). - Con đường thứ hai từ nhà An đến thư viện có độ dài
b(đơn vị). - Con đường thứ ba từ trường đến thư viện có độ dài
c(đơn vị).
An chỉ di chuyển trên các con đường này để hoàn thành hành trình của mình.
Yêu cầu: Hãy tính độ dài hành trình ngắn nhất mà An thực hiện trong một ngày.
Dữ liệu
Nhập vào từ màn hình gồm 3 dòng, mỗi dòng chứa một số nguyên lần lượt là giá trị của a, b và c
(1 ≤ a, b, c ≤ 10^6)
Kết quả
In ra màn hình duy nhất một số nguyên là độ dài ngắn nhất của hành trình An thực hiện.
Ví dụ
Input:
1
1
3
Output:
4
Giải thích ví dụ
- Đường từ nhà (H) → trường (S) độ dài = a = 1
- Đường từ trường (S) → thư viện (L) có thể đi trực tiếp độ dài = c = 3, hoặc đi vòng S → H → L với độ dài = a + b = 1 + 1 = 2. Do đó chọn 2.
- Đường từ thư viện (L) → nhà (H) có thể đi trực tiếp độ dài = b = 1, hoặc đi vòng L → S → H với độ dài = c + a = 3 + 1 = 4. Chọn 1.
Tổng = 1 + 2 + 1 = 4.
Trí tuệ nhân tạo
Nộp bàiPoint: 100
Bài 1: Trí tuệ nhân tạo (0,8 điểm)
Một trí tuệ nhân tạo cần kết nối với một máy chủ từ xa để đồng bộ hóa dữ
liệu. Máy chủ này hoạt động theo một chu kỳ cố định để bảo trì và tối ưu
hiệu năng: - X giây ở trạng thái Online (cho phép kết nối); - Sau
đó, S giây ở trạng thái Offline (từ chối mọi kết nối).
Chu kỳ này lặp lại liên tục và bắt đầu từ giây thứ 1 với trạng thái Online.
Yêu cầu
Một trí tuệ nhân tạo gửi yêu cầu kết nối đến máy chủ vào giây thứ T.
Hãy kiểm tra tại giây thứ T, máy chủ đang ở trạng thái "Online" hay
"Offline"?
Dữ liệu vào:
- Dòng đầu tiên gồm số nguyên dương
X(1 ≤ X ≤ 10\^9); - Dòng thứ hai gồm số nguyên dương
S(1 ≤ S ≤ 10\^9); - Dòng thứ ba gồm số nguyên dương
T(1 ≤ T ≤ 10\^9).
Kết quả:
- Nếu tại giây thứ
Tmáy chủ đang "Offline" ghi ra số0, - Nếu tại giây thứ
Tmáy chủ đang "Online" ghi ra số1.
Ví dụ
Input:
5
7
5
Output:
1
Input:
5
7
20
Output:
0
Ràng buộc
- Có 80% số test ứng với 80% số điểm có
T ≤ 10^6; - 20% số test còn lại ứng với 20% số điểm không có ràng buộc thêm.
Tính số ngày thắp sáng đèn Trung Thu
Nộp bàiPoint: 100
Tính số ngày thắp sáng đèn Trung Thu
Trong dịp lễ Trung Thu, khu phố treo đèn lồng màu vàng và đỏ dọc theo tuyến phố.
Mỗi ngày đèn đều được treo, nhưng chỉ thắp sáng vào ban đêm.
Quy định của khu phố:
- Cứ sau m ngày treo liên tiếp thì phải có 1 ngày tắt đèn để tiết kiệm điện.
- Lễ hội bắt đầu từ ngày thứ
ktrong tuần và kéo dài liên tiếpdngày.
Yêu cầu
Tính số ngày đèn được thắp sáng trong suốt lễ hội kéo dài d ngày.
Dữ liệu nhập vào
Gồm 3 dòng, mỗi dòng ghi một số tự nhiên, lần lượt là:
k: ngày bắt đầu (2 ≤ k ≤ 8), trong đó 2 là thứ hai, 3 là thứ ba, …, 8 là chủ nhật.d: số ngày kéo dài của lễ hội (1 ≤ d ≤ 10^15).m: số ngày treo liên tiếp trước khi tắt đèn 1 ngày (2 ≤ m ≤ 7).
Kết quả
- Một số nguyên duy nhất: số ngày đèn được thắp sáng trong dịp lễ.
Ví dụ
Ví dụ 1
Dữ liệu:
5
10
3
Kết quả:
8
Giải thích:
Trong 10 ngày, cứ 3 ngày thắp sáng → 1 ngày tắt.
→ Có 2 ngày tắt → 10 - 2 = 8 ngày thắp sáng.
Ví dụ 2
Dữ liệu:
7
7
4
Kết quả:
6
Giải thích:
Trong 7 ngày, cứ 4 ngày thắp sáng → 1 ngày tắt.
→ Có 1 ngày tắt → 7 - 1 = 6 ngày thắp sáng.
Chấm điểm
- Subtask 1 (50% số điểm): d ≤ 1000
- Subtask 2 (50% số điểm): 1000 < d ≤ 10^15
Lưới ô vuông 2
Nộp bàiPoint: 100
Tính tổng trên vòng chứa K – Bảng xoắn ốc
Cho một bảng hình vuông kích thước (2 x N - 1).
Các số tự nhiên bắt đầu từ 1 được điền theo chiều xoắn ốc từ ngoài vào trong.
Bảng chia thành đúng N vòng (layer):
| Vòng | Số ô trong vòng |
|---|---|
| 1 | 1 ô trung tâm |
| 2 | 8 ô bao quanh vòng 1 |
| 3 | 16 ô bao quanh vòng 2 |
| … | … |
| N | ô trên viền ngoài cùng |
Minh hoạ khi N = 4:
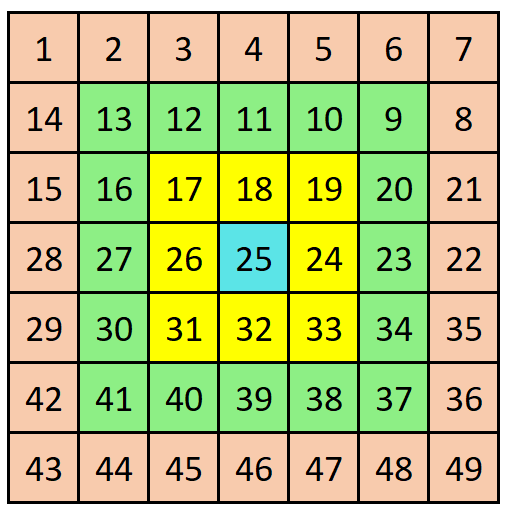
Bài toán
Cho số nguyên dương K. Hãy tính tổng của toàn bộ các ô thuộc vòng thứ K.
In kết quả mod 10007.
Input Specification
Dòng 1: N (1 ≤ N ≤ 10^9)
Dòng 2: K (K ≤ N)
Output Specification
In ra (tổng của vòng chứa K) mod 10007.
Sample
Input
4
2
Output
200
Ghi chú
- Với (N = 4), vòng 2 (màu xanh lá) gồm 8 + 8 = 16 ô, tổng của chúng bằng 200.
- Số ô trên vòng thứ (i):
- Nếu (i = 1): 1 ô.
- Nếu (i ≥ 2): (8(i-1)) ô.
- Có thể tìm công thức tổng khối xoắn ốc hoặc sinh gọn bằng cấp số cộng; chỉ cần giữ phần dư 10007.
Đèn lồng
Nộp bàiPoint: 100
Bài 2. Đèn lồng (5,0 điểm)
Nhân dịp Tết Trung thu, khu phố đã treo N chiếc đèn lồng có màu vàng
và màu đỏ, từ trái sang phải. Một dãy đèn lồng liên tiếp được gọi là
"đẹp" nếu số lượng đèn màu vàng gấp đôi số lượng đèn màu đỏ.
Yêu cầu
Cho một xâu S chỉ gồm các ký tự 'V' và 'D' mô tả dãy đèn lồng, ký
tự 'V' mô tả đèn lồng màu vàng và ký tự 'D' mô tả đèn lồng màu đỏ.
Hãy tìm độ dài của dãy đèn lồng "đẹp" dài nhất.
Dữ liệu vào:
- Một xâu
Schỉ gồm các ký tự'V'và'D'mô tả dãy đèn có độ dài không vượt quá 10^5.
Kết quả :
- Một số nguyên duy nhất là kết quả của bài toán.
Ví dụ
Input :
VDVVDDVVD
Output :
6
Giải thích:\ Dãy đèn lồng "đẹp" dài nhất được in đậm: VDVVDDVVD.
Ràng buộc
- Có 60% số test ứng với 60% số điểm có độ dài xâu
Skhông vượt quá 100; - 20% số test khác ứng với 20% số điểm có độ dài xâu
Skhông vượt quá 1000; - 20% số test còn lại ứng với 20% số điểm không có ràng buộc thêm.
Số nhỏ nhất chia hết cho 4
Nộp bàiPoint: 100
Đề bài: Thay đổi tối đa 2 chữ số để được số nhỏ nhất chia hết cho 4
Mô tả: Cho một số tự nhiên N. Bạn được phép thay đổi tối đa 2 chữ số của N (ở bất kỳ vị trí nào) để thu được số nhỏ nhất chia hết cho 4. Hãy in ra số thu được.
Dữ liệu vào
- Một dòng chứa số tự nhiên N (không quá 15 chữ số, 10 <= N <= 10^15).
Kết quả
- Một số – kết quả nhỏ nhất chia hết cho 4 có thể thu được bằng cách đổi tối đa 2 chữ số của N.
- Nếu N ban đầu đã chia hết cho 4 thì kết quả là chính N.
- Nếu không thể thu được số chia hết cho 4 sau tối đa 2 lần đổi, in ra -1.
Ví dụ
Input
178
Output
100
Giải thích:
- Đổi hai chữ số cuối của 178: 7 → 0, 8 → 0 để được 100, đây là số nhỏ nhất chia hết cho 4 với tối đa 2 phép đổi.